Getting a Handle on Fraction-to-Decimal Conversions
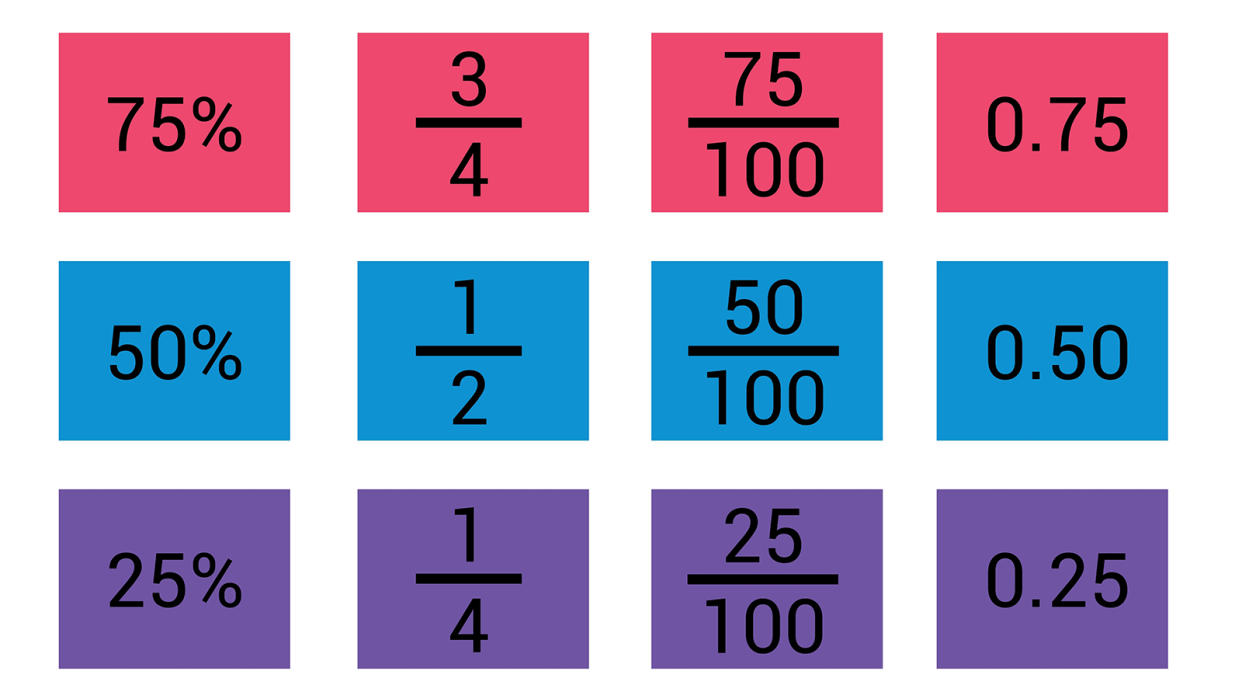
As you might recall from math class, fractions and decimals are two different ways of representing the same thing. A third option, percentages, is a close cousin of decimals. However, making use of this knowledge requires knowing how to convert one into the other.
Fraction to decimal conversion can be an opportunity to deepen your understanding of numbers and math. Sometimes the process will take more work, and sometimes less, but the operation is relatively straightforward.
What Are Fractions?
Fractions represent a division problem. If you look at the fraction 1/4, you can think of the line between the numbers (sometimes simply referred to as the "line," and sometimes as the "fraction bar") as a division sign.
That means that 1/4 is, in essence, saying "1 divided by 4."
That's all that fractions are. The top number, called the "numerator," is being divided by the bottom number, which is known as the "denominator." To calculate the decimal equivalent, you simply divide the numerator by the denominator, and you'll have your answer (which is 0.25, in this case).
The Case of Improper Fractions
If you're not a math maven, the sudden appearance of "improper" in the conversation might give you the heebie-jeebies. It may even trigger flashbacks of rational versus irrational numbers, as well as unpleasant memories of math exams.
Fear not! In this case, the phrase has a straightforward meaning: Whenever a fraction has a higher value numerator than denominator, you're looking at a so-called "improper fraction." This means that you're dealing with a number that is greater than 1.
This should make some intuitive sense, since the word "fraction" literally means "part of a whole." (In standard English, a "fraction" of something tends to connote a very small portion of that thing, but the essence is the same; it's a part, not the whole thing.)
Therefore, improper fractions are fractions that are more than a whole, such as 27/14 or 5/3.
What Are Decimals?
A decimal is another way to represent a fraction — or, put differently, another way to write the part of a whole number. If we look back at the previous example of 1/4, we'll see that, if you divide 4 by 1, you'll get 0.25, which is the decimal equivalent of the fraction.
We haven't yet done the math problem that gives us the correct answer, but you're probably aware that 1/4, also known as a "quarter" or a "fourth," is 0.25. This is fairly easy to remember, since the coin we call the "quarter" has a value of 25 cents, and 4 of them together equal 1 dollar, or 100 cents.
You can also add them up:
25 + 25 + 25 + 25 = 100
Going From Fraction to Decimal With a Calculator
Probably the easiest way to converting a fraction to decimal is to use a calculator. Chances are, you have a calculator app on your phone, and if you don't, you might still have a cheap calculator rattling around in a desk drawer.
Since you're now aware that a fraction is a straightforward division problem, once you've got your calculator at the ready, you can complete the necessary steps.
Let's start with 3/8. If you type "3 ÷ 8" into the calculator app, you'll get the decimal form: 0.375.
One nifty thing about calculators is their ability to handle some very big (or very small) numbers with ease. If you wanted to do the fraction to decimal conversion of 45/72, you would find your answer an instant.
Simply type 45 ÷ 72, and you'll get 0.625.
What Is a Repeating Decimal?
Not every fraction to decimal conversion yields a short string of numbers. Sometimes, you wind up with repeating decimals. Take the case of 2/3. If you type 2 ÷ 3 into your calculator, you'll get 0.66666666 and so on, for as many digits as your screen will allow.
This is a repeating decimal. Other fraction to decimal conversions that give you repeating digits are:
1/3 = 0.333333333333
4/9 = 0.444444444444
7/11 = 0.636363636363
2/7 = 0.285714285714
Converting Fractions to Decimals Using Long Division
Here's the part that might require a refresher with grade-school mathematics. But don't stress: You'll find that once you get the basics of long division, you'll be every bit the decimal calculator that your phone now is. It will also require paper and a pencil, or anything to write with.
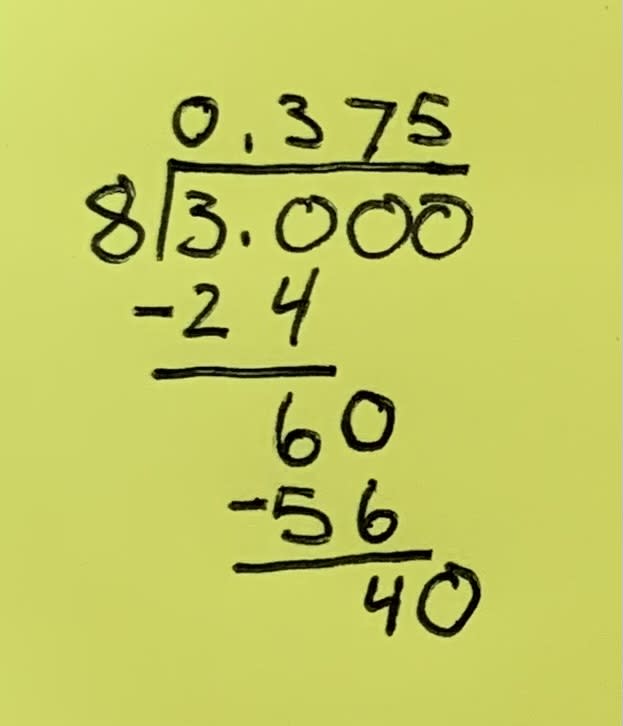
Let's dive into long division with a clear example. We'll use 3/8 to walk through this step-by-step process. Recall that 3/8 is equivalent to 3 ÷ 8.
Set up the problem. Write the numerator (now called the dividend) 3 under the division bar and the divisor (formerly, the denominator) 8 outside the bar.
Divide. But wait: 8 doesn't go into 3 evenly; 8 is a larger number than 3 (which is why we're getting fractions, not whole numbers, right?) .
Add a 0. We get around this problem by adding a 0 after the 3. Now we're dealing with the more straightforward task of dividing 30 by 8.
Divide again. How many times does 8 go into 30? Well, it goes in 3 times — not evenly (3 x 8 = 24), but that's okay. 24 is less than 30.
Add a decimal. Put a decimal point before the 3 on top of the division bar. This is important, and it's what makes this fraction to decimal conversion work.
Multiply. Multiplying the quotient (3) by the divisor (8) gives us an answer of 24: (3 x 8 = 24). Write 24 under the 30.
Subtract. Subtract 24 from 30 to get 6. Draw a line under the 24, subtract, and write 6 below the line.
Add another zero to the dividend. Now, bring down the 0, to sit next to the 6, making 60.
Repeat the steps. 8 goes into 60 seven times (8 x 7 = 56), so write 7 above the bar next to the 3. Subtract 56 from 60 to get 4. Now, follow the same process you used in steps 1 through 8 and bring down the next zero. This gives you 40.
Keep going until you have no remainder. Luckily for us, in this example, you're already there once you've reached that 40. 8 goes into 40 a clean 5 times. Put that 5 next to the 7, and you'll have your answer: 0.375.
Now you can say you know how to convert fractions to decimals using long division!
How to Convert a Fraction to a Percent
Luckily, adding percentages to the mix doesn't make things significantly more complex. In fact, once you become sufficiently comfortable with the fraction to decimal process, you really have only one more step to take.
In a sense, the decimal equivalent of a fraction is already a percent. All you have to do to make it official is to move the decimal point two positions to the right.
If you take the above example of 3/8, we know that the answer is .375. By shifting the decimal point two places to the right, you get 37.5. Now all that's left to do is throw a percentage sign (%) after the number.
3/8 = 37.5%
Fraction-Decimal Conversion Chart
Here are some common conversions in a handy-dandy reference chart.
Fraction | Decimal | Percent |
1/10 | 0.1 | 10% |
1/5 | 0.2 | 20% |
1/4 | 0.25 | 25% |
3/10 | 0.3 | 30% |
1/3 | 0.33 | 33.3% |
2/5 | 0.4 | 40% |
1/2 | 0.5 | 50% |
3/5 | 0.6 | 60% |
2/3 | 0.66 | 66.6% |
7/10 | 0.7 | 70% |
3/4 | 0.75 | 75% |
4/5 | 0.8 | 80% |
9/10 | 0.9 | 90% |
Original article: Getting a Handle on Fraction-to-Decimal Conversions
Copyright © 2024 HowStuffWorks, a division of InfoSpace Holdings, LLC, a System1 Company


