Black holes are mysterious, yet also deceptively simple − a new space mission may help physicists answer hairy questions about these astronomical objects

Physicists consider black holes one of the most mysterious objects that exist. Ironically, they’re also considered one of the simplest. For years, physicists like me have been looking to prove that black holes are more complex than they seem. And a newly approved European space mission called LISA will help us with this hunt.
Research from the 1970s suggests that you can comprehensively describe a black hole using only three physical attributes – their mass, charge and spin. All the other properties of these massive dying stars, like their detailed composition, density and temperature profiles, disappear as they transform into a black hole. That is how simple they are.
The idea that black holes have only three attributes is called the “no-hair” theorem, implying that they don’t have any “hairy” details that make them complicated.
Hairy black holes?
For decades, researchers in the astrophysics community have exploited loopholes or work-arounds within the no-hair theorem’s assumptions to come up with potential hairy black hole scenarios. A hairy black hole has a physical property that scientists can measure – in principle – that’s beyond its mass, charge or spin. This property has to be a permanent part of its structure.
About a decade ago, Stefanos Aretakis, a physicist currently at the University of Toronto, showed mathematically that a black hole containing the maximum charge it could hold – called an extremal charged black hole – would develop “hair” at its horizon. A black hole’s horizon is the boundary where anything that crosses it, even light, can’t escape.
Aretakis’ analysis was more of a thought experiment using a highly simplified physical scenario, so it’s not something scientists expect to observe astrophysically. But supercharged black holes might not be the only kind that could have hair.
Since astrophysical objects such as stars and planets are known to spin, scientists expect that black holes would spin as well, based on how they form. Astronomical evidence has shown that black holes do have spin, though researchers don’t know what the typical spin value is for an astrophysical black hole.
Using computer simulations, my team has recently discovered similar types of hair in black holes that are spinning at the maximum rate. This hair has to do with the rate of change, or the gradient, of space-time’s curvature at the horizon. We also discovered that a black hole wouldn’t actually have to be maximally spinning to have hair, which is significant because these maximally spinning black holes probably don’t form in nature.
Detecting and measuring hair
My team wanted to develop a way to potentially measure this hair – a new fixed property that might characterize a black hole beyond its mass, spin and charge. We started looking into how such a new property might leave a signature on a gravitational wave emitted from a fast-spinning black hole.
A gravitational wave is a tiny disturbance in space-time typically caused by violent astrophysical events in the universe. The collisions of compact astrophysical objects such as black holes and neutron stars emit strong gravitational waves. An international network of gravitational observatories, including the Laser Interferometer Gravitational-wave Observatory in the United States, routinely detects these waves.
Our recent studies suggest that one can measure these hairy attributes from gravitational wave data for fast-spinning black holes. Looking at the gravitational wave data offers an opportunity for a signature of sorts that could indicate whether the black hole has this type of hair.
Our ongoing studies and recent progress made by Som Bishoyi, a student on the team, are based on a blend of theoretical and computational models of fast-spinning black holes. Our findings have not been tested in the field yet or observed in real black holes out in space. But we hope that will soon change.
LISA gets a go-ahead
In January 2024, the European Space Agency formally adopted the space-based Laser Interferometer Space Antenna, or LISA, mission. LISA will look for gravitational waves, and the data from the mission could help my team with our hairy black hole questions.
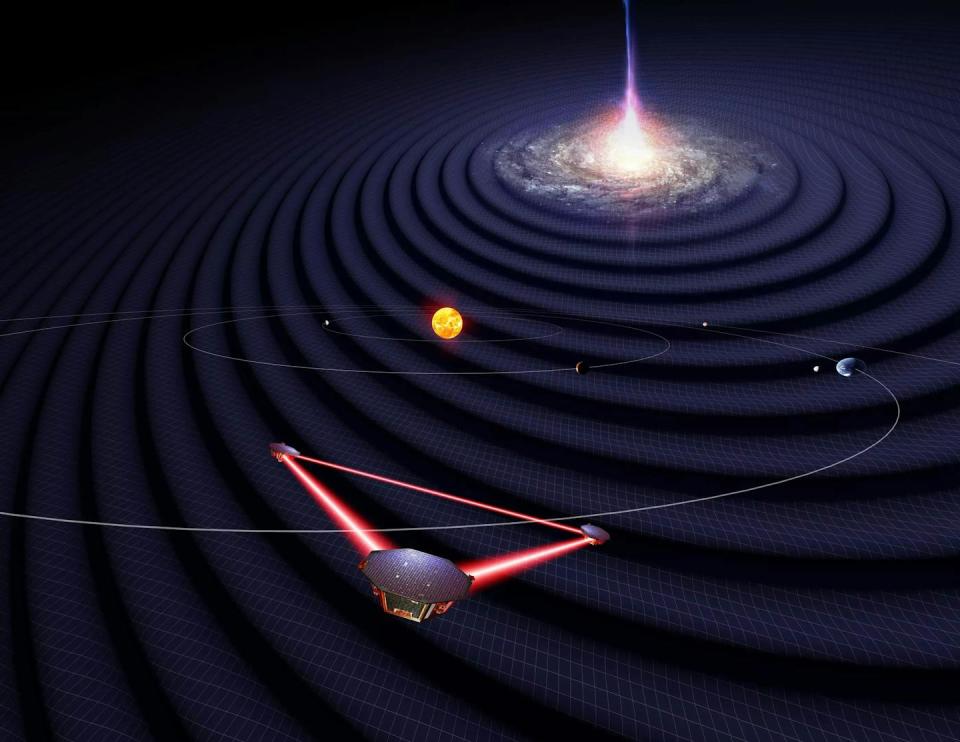
Formal adoption means that the project has the go-ahead to move to the construction phase, with a planned 2035 launch. LISA consists of three spacecrafts configured in a perfect equilateral triangle that will trail behind the Earth around the Sun. The spacecrafts will each be 1.6 million miles (2.5 million kilometers) apart, and they will exchange laser beams to measure the distance between each other down to about a billionth of an inch.
LISA will detect gravitational waves from supermassive black holes that are millions or even billions of times more massive than our Sun. It will build a map of the space-time around rotating black holes, which will help physicists understand how gravity works in the close vicinity of black holes to an unprecedented level of accuracy. Physicists hope that LISA will also be able to measure any hairy attributes that black holes might have.
With LIGO making new observations every day and LISA to offer a glimpse into the space-time around black holes, now is one of the most exciting times to be a black hole physicist.
This article is republished from The Conversation, a nonprofit, independent news organization bringing you facts and trustworthy analysis to help you make sense of our complex world. It was written by: Gaurav Khanna, University of Rhode Island
Read more:
The scariest things in the universe are black holes – and here are 3 reasons
Why are some black holes bigger than others? An astronomer explains how these celestial vacuums grow
The article presents work carried out in collaboration with Stefanos Aretakis, Kevin Gonzalez-Quesada, Lior Burko, Subir Sabharwal and Som Bishoyi. This research was supported by the US National Science Foundation. All computations were performed at the Massachusetts Green High Performance Computing Center leveraging the resources of the URI Center for Computational Research. The author also acknowledges support from the UMass-URI Gravity Research Consortium (U2GRC).


